% **Blog post code introduction**
%
% Congrats on activating the "All cells" option in this interactive blog post =D
%
% Below, several new HTML blocks have appears prior to the figures, displaying the Octave/MATLAB code that was used to generate the figures in this blog post.
%
% If you want to reproduce the data on your own local computer, you simply need to have qMRLab installed in your Octave/MATLAB path and run the "startup.m" file, as is shown below.
%
% If you want to get under the hood and modify the code right now, you can do so in the Jupyter Notebook of this blog post hosted on MyBinder. The link to it is in the introduction above.
Inversion Recovery T1 Mapping
Widely considered the gold standard for T1 mapping, the inversion recovery technique estimates T1 values by fitting the signal recovery curve acquired at different delays after an inversion pulse (180°). In a typical inversion recovery experiment (Figure 1), the magnetization at thermal equilibrium is inverted using a 180° RF pulse. After the longitudinal magnetization recovers through spin-lattice relaxation for predetermined delay (“inversion time”, TI), a 90° excitation pulse is applied, followed by a readout imaging sequence (typically a spin-echo or gradient-echo readout) to create a snapshot of the longitudinal magnetization state at that TI.
Inversion recovery was first developed for NMR in the 1940s (Hahn 1949; Drain 1949), and the first T1 map was acquired using a saturation-recovery technique (90° as a preparation pulse instead of 180°) by (Pykett and Mansfield 1978). Some distinct advantages of inversion recovery are its large dynamic range of signal change and an insensitivity to pulse sequence parameter imperfections (Stikov et al. 2015). Despite its proven robustness at measuring T1, inversion recovery is scarcely used in practice, because conventional implementations require repetition times (TRs) on the order of 2 to 5 T1 (Steen et al. 1994), making it challenging to acquire whole-organ T1 maps in a clinically feasible time. Nonetheless, it is continuously used as a reference measurement during the development of new techniques, or when comparing different T1 mapping techniques, and several variations of the inversion recovery technique have been developed, making it practical for some applications (Messroghli et al. 2004; Piechnik et al. 2010).

Signal Modelling
The steady-state longitudinal magnetization of an inversion recovery experiment can be derived from the Bloch equations for the pulse sequence {θ180 – TI – θ90 – (TR-TI)}, and is given by:

where Mz is the longitudinal magnetization prior to the θ90 pulse. If the in-phase real signal is desired, it can be calculated by multiplying Eq. 1 by ksin(θ90)e-TE/T2, where k is a constant. This general equation can be simplified by grouping together the constants for each measurements regardless of their values (i.e. at each TI, same TE and θ90 are used) and assuming an ideal inversion pulse:

where the first three terms and the denominator of Eq. 1 have been grouped together into the constant C. If the experiment is designed such that TR is long enough to allow for full relaxation of the magnetization (TR > 5T1), we can do an additional approximation by dropping the last term in Eq. 2:
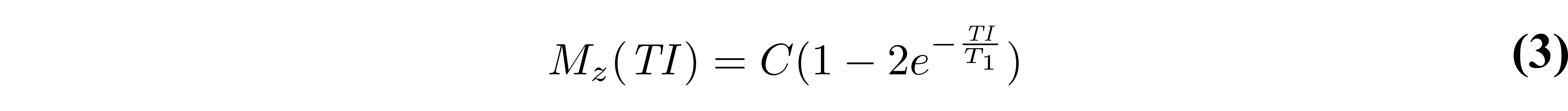
The simplicity of the signal model described by Eq. 3, both in its equation and experimental implementation, has made it the most widely used equation to describe the signal evolution in an inversion recovery T1 mapping experiment. The magnetization curves are plotted in Figure 2 for approximate T1 values of three different tissues in the brain. Note that in many practical implementations, magnitude-only images are acquired, so the signal measured would be proportional to the absolute value of Eq. 3.
Figure 2. Inversion recovery curves (Eq. 2) for three different T1 values, approximating the main types of tissue in the brain.
%% MATLAB/OCTAVE CODE
% Adds qMRLab to the path of the environment
cd ../qMRLab
startup
%% MATLAB/OCTAVE CODE
% Code used to generate the data required for Figure 2 of the blog post
clear all
%% Setup parameters
% All times are in seconds
% All flip angles are in degrees
params.TR = 5.0;
params.TI = linspace(0.001, params.TR, 1000);
params.TE = 0.004;
params.T2 = 0.040;
params.EXC_FA = 90; % Excitation flip angle
params.INV_FA = 180; % Inversion flip angle
params.signalConstant = 1;
%% Calculate signals
%
% The option 'GRE-IR' selects the analytical equations for the gradient echo readout inversion recovery experiment
% The option '4' is a flag that selects the long TR approximation of the analytical solution (TR>>T1), Eq. 3 of the blog post.
%
% To see all the options available, run `help inversion_recovery.analytical_solution`
% White matter
params.T1 = 0.900; % in seconds
signal_WM = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);
% Grey matter
params.T1 = 1.500; % in seconds
signal_GM = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);
% CSF
params.T1 = 4.000; % in seconds
signal_CSF = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);
Practically, Eq. 1 is the better choice for simulating the signal of an inversion recovery experiment, as the TRs are often chosen to be greater than 5T1 of the tissue-of-interest, which rarely coincides with the longest T1 present (e.g. TR may be sufficiently long for white matter, but not for CSF which could also be present in the volume). Equation 3 also assumes ideal inversion pulses, which is rarely the case due to slice profile effects. Figure 3 displays the inversion recovery signal magnitude (complete relaxation normalized to 1) of an experiment with TR = 5 s and T1 values ranging between 250 ms to 5 s, calculated using both equations.
Figure 3. Signal recovery curves simulated using Eq. 3 (solid) and Eq. 1 (dotted) with a TR = 5 s for T1 values ranging between 0.25 to 5 s.
%% MATLAB/OCTAVE CODE
% Code used to generate the data required for Figure 3 of the blog post
clear all
%% Setup parameters
% All times are in seconds
% All flip angles are in degrees
params.TR = 5.0;
params.TI = linspace(0.001, params.TR, 1000);
params.TE = 0.004;
params.T2 = 0.040;
params.EXC_FA = 90; % Excitation flip angle
params.INV_FA = 180; % Inversion flip angle
params.signalConstant = 1;
T1_range = 0.25:0.25:5; % in seconds
%% Calculate signals
%
% The option 'GRE-IR' selects the analytical equations for the gradient echo readout inversion recovery experiment
% The option '1' is a flag that selects full analytical solution equation (no approximation), Eq. 1 of the blog post.
% The option '4' is a flag that selects the long TR approximation of the analytical solution (TR>>T1), Eq. 3 of the blog post.
%
% To see all the options available, run `help inversion_recovery.analytical_solution`
for ii = 1:length(T1_range)
params.T1 = T1_range(ii);
signal_T1_Eq1{ii} = inversion_recovery.analytical_solution(params, 'GRE-IR', 1);
signal_T1_Eq3{ii} = inversion_recovery.analytical_solution(params, 'GRE-IR', 4);
end
Data Fitting
Several factors impact the choice of the inversion recovery fitting algorithm. If only magnitude images are available, then a polarity-inversion is often implemented to restore the non-exponential magnitude curves (Figure 3) into the exponential form (Figure 2). This process is sensitive to noise due to the Rician noise creating a non-zero level at the signal null. If phase data is also available, then a phase term must be added to the fitting equation (Barral et al. 2010). Equation 3 must only be used to fit data for the long TR regime (TR > 5T1), which in practice is rarely satisfied for all tissues in subjects.
Early implementations of inversion recovery fitting algorithms were designed around the computational power available at the time. These included the “null method” (Pykett et al. 1983), assuming that each T1 value has unique zero-crossings (see Figure 2), and linear fitting of a rearranged version of Eq. 3 on a semi-log plot (Fukushima & Roeder 1981). Nowadays, a non-linear least-squares fitting algorithm (e.g. Levenberg-Marquardt) is more appropriate, and can be applied to either approximate or general forms of the signal model (Eq. 3 or Eq. 1). More recent work (Barral et al. 2010) demonstrated that T1 maps can also be fitted much faster (up to 75 times compared to Levenberg-Marquardt) to fit Eq. 1 – without a precision penalty – by using a reduced-dimension non-linear least squares (RD-NLS) algorithm. It was demonstrated that the following simplified 5-parameter equation can be sufficient for accurate T1 mapping:
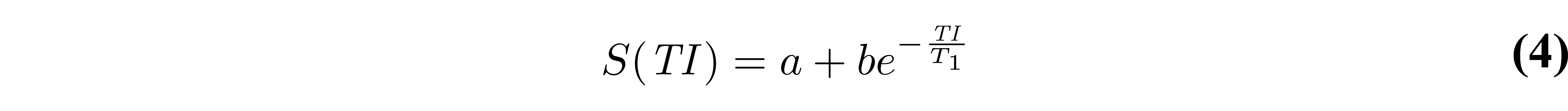
where a and b are complex values. If magnitude-only data is available, a 3-parameter model can be sufficient by taking the absolute value of Eq. 4. While the RD-NLS algorithms are too complex to be presented here (the reader is referred to the paper, (Barral et al. 2010)), the code for these algorithms was released open-source along with the original publication, and is also available as a qMRLab T1 mapping model. One important thing to note about Eq. 4 is that it is general – no assumption is made about TR – and is thus as robust as Eq. 1 as long as all pulse sequence parameters other than TI are kept constant between each measurement. Figure 4 compares simulated data (Eq. 1) using a range of TRs (1.5T1 to 5T1) fitted using either RD-NLS & Eq. 4 or a Levenberg-Marquardt fit of Eq. 2.
Figure 4. Fitting comparison of simulated data (blue markers) with T1 = 1 s and TR = 1.5 to 5 s, using fitted using RD-NLS & Eq. 4 (green) and Levenberg-Marquardt & Eq. 2 (orange, long TR approximation).
%% MATLAB/OCTAVE CODE
% Code used to generate the data required for Figure 4 of the blog post
clear all
%% Setup parameters
% All times are in milliseconds
% All flip angles are in degrees
params.TI = 50:50:1500;
TR_range = 1500:50:5000;
params.EXC_FA = 90;
params.INV_FA = 180;
params.T1 = 1000;
%% Calculate signals
%
% The option 'GRE-IR' selects the analytical equations for the gradient echo readout inversion recovery experiment
% The option '1' is a flag that selects full analytical solution equation (no approximation), Eq. 1 of the blog post.
%
% To see all the options available, run `help inversion_recovery.analytical_solution`
for ii = 1:length(TR_range)
params.TR = TR_range(ii);
Mz_analytical(ii,:) = inversion_recovery.analytical_solution(params, 'GRE-IR', 1);
end
%% Fit data using Levenberg-Marquardt with the long TR approximation equation
%
% The option '4' is a flag that selects the long TR approximation of the analytical solution (TR>>T1), Eq. 3 of the blog post.
%
% To see all the options available, run `help inversion_recovery.fit_lm`
for ii=1:length(TR_range)
fitOutput_lm{ii} = inversion_recovery.fit_lm(Mz_analytical(ii,:), params, 4);
T1_lm(ii) = fitOutput_lm{ii}.T1;
end
%% Fit data using the RDLS method (Barral), Eq. 4 of the blog post.
%
% Create a qMRLab inversion recovery model object and load protocol values
irObj = inversion_recovery();
irObj.Prot.IRData.Mat = params.TI';
for ii=1:length(TR_range)
data.IRData = Mz_analytical(ii,:);
fitOutput_barral{ii} = irObj.fit(data);
T1_barral(ii) = fitOutput_barral{ii}.T1;
end
Figure 5 displays an example brain dataset from an inversion recovery experiment, along with the T1 map fitted using the RD-NLS technique.
Figure 5. Figure 5. Example inversion recovery dataset of a healthy adult brain (left). Inversion times used to acquire this magnitude image dataset were 30 ms, 530 ms, 1030 ms, and 1530 ms, and the TR used was 1550 ms. The T1 map (right) was fitted using a RD-NLS algorithm.
%% MATLAB/OCTAVE CODE
% Download inversion recovery brain MRI data for Figure 5 of the blog post
cmd = ['curl -L -o ir_brain.zip https://osf.io/ezv74/download/'];
[STATUS,MESSAGE] = unix(cmd);
unzip('ir_brain.zip');
%% MATLAB/OCTAVE CODE
% Code used to generate the data required for Figure 5 of the blog post
clear all
% Load data into environment, and rotate mask to be aligned with IR data
load('IRData.mat');
load('IRMask.mat');
IRData = data;
Mask = imrotate(Mask,180);
clear data
% Format qMRLab inversion_recovery model parameters, and load them into the Model object
Model = inversion_recovery;
TI = [30; 530; 1030; 1530];
Model.Prot.IRData.Mat = [TI];
% Format data structure so that they may be fit by the model
data = struct();
data.IRData= double(IRData);
data.Mask= double(Mask);
FitResults = FitData(data,Model,0); % The '0' flag is so that no wait bar is shown.
%% MATLAB/OCTAVE CODE
% Code used to re-orient the images to make pretty figures, and to assign variables with the axis lengths.
T1_map = imrotate(FitResults.T1.*Mask,-90);
xAxis = [0:size(T1_map,2)-1];
yAxis = [0:size(T1_map,1)-1];
% Raw MRI data at different TI values
TI_0030 = imrotate(squeeze(IRData(:,:,:,1).*Mask),-90);
TI_0530 = imrotate(squeeze(IRData(:,:,:,2).*Mask),-90);
TI_1030 = imrotate(squeeze(IRData(:,:,:,3).*Mask),-90);
TI_1530 = imrotate(squeeze(IRData(:,:,:,4).*Mask),-90);
Benefits and Pitfalls
The conventional inversion recovery experiment is considered the gold standard T1 mapping technique for several reasons. A typical protocol has a long TR value and a sufficient number of inversion times for stable fitting (typically 5 or more) covering the range [0, TR]. It offers a wide dynamic range of signals (up to [-kM0, kM0]), allowing a number of inversion times where high SNR is available to sample the signal recovery curve (Fukushima 1981). T1 maps produced by inversion recovery are largely insensitive to inaccuracies in excitation flip angles and imperfect spoiling (Stikov et al. 2015), as all parameters except TI are constant for each measurement and only a single acquisition is performed (at TI) during each TR. One important pulse sequence design consideration is to avoid acquiring at inversion times where the signal for T1 values of the tissue-of-interest is nulled, as the magnitude images at this TI time will be dominated by Rician noise which can negatively impact the fit under low SNR circumstances (Figure 6). Inversion recovery can also often be acquired using commonly available standard pulse sequences available on most MRI scanners by setting up a customized acquisition protocol, and does not require any additional calibration measurements.
Figure 6. Monte Carlo simulations (mean and standard deviation (STD), blue markers) and fitted T1 values (mean and STD, red and green respectively) generated for a T1 value of 900 ms and 5 TI values linearly spaced across the TR (ranging from 1 to 5 s). A bump in T1 STD occurs near TR = 3000 ms, which coincides with the TR where the second TI is located near a null point for this T1 value.
%% MATLAB/OCTAVE CODE
% Code used to generate the data required for Figure 6 of the blog post
clear all
%% Setup parameters
% All times are in seconds
% All flip angles are in degrees
TR_range = 1000:100:5000; % in seconds
x = struct;
x.T1 = 900; % in seconds
Opt.SNR = 25;
Opt.M0 = 1;
Opt.FAexcite = 90; % Excitation flip angle
Opt.FAinv = 180; % Inversion flip angle
%% Monte Carlo data simulation
% Simulate noisy signal data 1,000 time, fit the data, then calculate the means and standard deviations of the data and fitted T1
% Data is calculated by calculating the a and b values of Eq. 4 from the full analytical equations (Eq. 1)
Model = inversion_recovery;
for ii = 1:length(TR_range)
Opt.TR = TR_range(ii);
Opt.T1 = x.T1;
TI_lowres(ii,:) = linspace(0.05, Opt.TR, 6)';
Model.Prot.IRData.Mat = [TI_lowres(ii,:)];
[ra,rb] = Model.ComputeRaRb(x,Opt);
x.rb = rb;
x.ra = ra;
for jj = 1:1000
[FitResult{ii,jj}, noisyData{ii,jj}] = Model.Sim_Single_Voxel_Curve(x,Opt,0);
fittedT1(ii,jj) = FitResult{ii,jj}.T1;
noisyData_array(ii,jj,:) = noisyData{ii,jj}.IRData;
end
for kk=1:length(TI_lowres(ii,:))
data_mean(ii,kk) = mean(noisyData_array(ii,:,kk));
data_std(ii,kk) = std(noisyData_array(ii,:,kk));
end
T1_mean(ii) = mean(fittedT1(ii,:));
T1_std(ii) = std(fittedT1(ii,:));
end
%% Calculate the noiseless data at a higher TI resolution to plot the ideal signal curve.
%
for ii = 1:length(TR_range)
TI_highres(ii,:) = linspace(0.05, TR_range(ii), 500);
Model.Prot.IRData.Mat = [TI_highres(ii,:)];
Opt.TR = TR_range(ii);
Opt.T1 = x.T1;
[ra,rb] = Model.ComputeRaRb(x,Opt);
x.rb = rb;
x.ra = ra;
data_noiseless(ii,:) = Model.equation(x);
end
Despite a widely acknowledged robustness for measuring accurate T1 maps, inversion recovery is not often used in studies. An important drawback of this technique is the need for long TR values, generally on the order of a few T1 for general models (e.g. Eqs. 1 and 4), and up to 5T1 for long TR approximated models (Eq. 3). It takes about to 10-25 minutes to acquire a single-slice T1 map using the inversion recovery technique, as only one TI is acquired per TR (2-5 s) and conventional cartesian gradient readout imaging acquires one phase encode line per excitation (for a total of ~100-200 phase encode lines). The long acquisition time makes it challenging to acquire whole-organ T1 maps in clinically feasible protocol times. Nonetheless, it is useful as a reference measurement for comparisons against other T1 mapping methods, or to acquire a single-slice T1 map of a tissue to get T1 estimates for optimization of other pulse sequences.
Other Saturation-Recovery T1 Mapping techniques
Several variations of the inversion recovery pulse sequence were developed to overcome challenges like those specified above. Amongst them, the Look-Locker technique (Look and Locker 1970) stands out as one of the most widely used in practice. Instead of a single 90° acquisition per TR, a periodic train of small excitation pulses θ are applied after the inversion pulse, {θ180 – 𝛕 – θ – 𝛕 – θ – ...}, where 𝛕 = TR/n and n is the number of sampling acquisitions. This pulse sequence samples the inversion time relaxation curve much more efficiently than conventional inversion recovery, but at a cost of lower SNR. However, because the magnetization state of each TI measurement depends on the previous series of θ excitation, it has higher sensitivity to B1-inhomogeneities and imperfect spoiling compared to inversion recovery (Gai et al. 2013; Stikov et al. 2015) . Nonetheless, Look-Locker is widely used for rapid T1 mapping applications, and variants like MOLLI (Modified Look-Locker Inversion recovery) and ShMOLLI (Shortened MOLLI) are widely used for cardiac T1 mapping (Messroghli et al. 2004; Piechnik et al. 2010)
Another inversion recovery variant that’s worth mentioning is saturation recovery, in which the inversion pulse is replaced with a saturation pulse: {θ90 – TI – θ90}. This technique was used to acquire the very first T1 map (Pykett and Mansfield 1978). Unlike inversion recovery, this pulse sequence does not need a long TR to recover to its initial condition; every θ90 pulse resets the longitudinal magnetization to the same initial state. However, to properly sample the recovery curve, TIs still need to reach the order of ~T1, the dynamic range of signal potential is cut in half ([0, M0]), and the short TIs (which have the fastest acquisition times) have the lowest SNRs.
Works Cited
Barral JK, Gudmundson E, Stikov N, et al. (2010) A robust methodology for in vivo T1 mapping. Magn. Reson. Med. 64(4): 1057–1067.
Drain LE (1949) A Direct Method of Measuring Nuclear Spin-Lattice Relaxation Times. Proceedings of the Physical Society. Section A 62(5): 301–306.
Fukushima, E. & Roeder, S., 1981. Experimental Pulse NMR. A Nuts and Bolts Approach, Reading, Massachusetts : Addison-Wesley Publ. Comp., Inc.
Gai, N.D. et al., 2013. Modified Look-Locker T1 evaluation using Bloch simulations: human and phantom validation. Magn. Reson. Med., 69(2), pp.329–336.
Hahn, E.L., 1949. An Accurate Nuclear Magnetic Resonance Method for Measuring Spin-Lattice Relaxation Times. Physics Review, 76(1), pp.145–146.
Look, D.C. & Locker, D.R., 1970. Time Saving in Measurement of NMR and EPR Relaxation Times. The Review of scientific instruments, 41(2), pp.250–251.
Messroghli, D.R. et al., 2004. Modified Look-Locker inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magn. Reson. Med., 52(1), pp.141–146.
Piechnik, S.K. et al., 2010. Shortened Modified Look-Locker Inversion recovery (ShMOLLI) for clinical myocardial T1-mapping at 1.5 and 3 T within a 9 heartbeat breathhold. J. Cardiovasc. Magn. Reson., 12, p.69.
Pykett, I.L. et al., 1983. Measurement of spin-lattice relaxation times in nuclear magnetic resonance imaging. Physics in medicine and biology, 28(6), pp.723–729.
Pykett, I.L. & Mansfield, P., 1978. A line scan image study of a tumorous rat leg by NMR. Physics in medicine and biology, 23(5), pp.961–967.
Steen, R.G. et al., 1994. Precise and accurate measurement of proton T1 in human brain in vivo: validation and preliminary clinical application. J. Magn. Reson. Imaging, 4(5), pp.681–691.
Stikov, N. et al., 2015. On the accuracy of T1 mapping: Searching for common ground. Magn. Reson. Med., 73(2), pp.514–522.
# PYTHON CODE
display(HTML(
'<style type="text/css">'
'.output_subarea {'
'display: block;'
'margin-left: auto;'
'margin-right: auto;'
'}'
'.blog_body {'
'line-height: 2;'
'font-family: timesnewroman;'
'font-size: 18px;'
'margin-left: 0px;'
'margin-right: 0px;'
'}'
'.biblio_body {'
'line-height: 1.5;'
'font-family: timesnewroman;'
'font-size: 18px;'
'margin-left: 0px;'
'margin-right: 0px;'
'}'
'.note_body {'
'line-height: 1.25;'
'font-family: timesnewroman;'
'font-size: 18px;'
'margin-left: 0px;'
'margin-right: 0px;'
'color: #696969'
'}'
'.figure_caption {'
'line-height: 1.5;'
'font-family: timesnewroman;'
'font-size: 16px;'
'margin-left: 0px;'
'margin-right: 0px'
'</style>'
))